Wstęp
Zasada najmniejszego działania pozwala na zupełnie inne spojrzenie na mechanikę klasyczną. W sformułowaniu Newtona, ruch ciała jest dany za pomocą równania stanowiącego treść II zasady dynamiki: \begin{equation} m\ddot{\mathbf{r}} = \sum_i \mathbf{F}_i. \end{equation} Jego rozwiązaniem, przy danych wartościach początkowych \(\mathbf{r}\) i \(\dot{\mathbf{r}}\), jest funkcja \(\mathbf{r}(t)\), czyli tor ruchu ciała. Zasada najmniejszego działania również udziela odpowiedzi na pytanie jaki jest tor ruchu ciała, jednak jej sformułowanie jest zupełnie inne. Mówi ona, że ciało między dwoma punktami porusza się tak, że pewna wielkość, zwana działaniem jest minimalna.
Zauważmy, że jej sformułowanie jest podobne do zasady Fermata, która mówi, że promień światła przemieszcza się po takie drodze, na której przebycie wymagany czas jest minimalny. W obydwu przypadkach mamy do czynienia z zasadą w pewnym sensie globalną, bowiem w obydwu przypadkach operujemy na wielkości charakteryzującej cały ,,tor’’ ruchu.
Zasada najmniejszego działania
Według zasady najmniejszego działania, ciało porusza się po trajektorii, dla której różnica między średnią energią kinetyczną a średnią energią potencjalną jest minimalna, tzn. wielkość \begin{equation} S = \int_{t_1}^{t_2}{(T - V)} dt \end{equation} przyjmuje wartość minimalną. Umówmy się również, że we wszystkich rozważaniach ruch ciała odbywa się w jednym wymiarze.
Weźmy pod uwagę najprostszy możliwy przypadek, aby zobaczyć, że przewidywania tej reguły są zgodne z oczekiwaniami. Dla ciała, które nie znajduje się pod wpływem żadnych sił, oczekujemy, że będzie się ono poruszało ruchem jednostajnym z szybkością \(v_0=(x_2-x_1)/(t_2-t_1)\).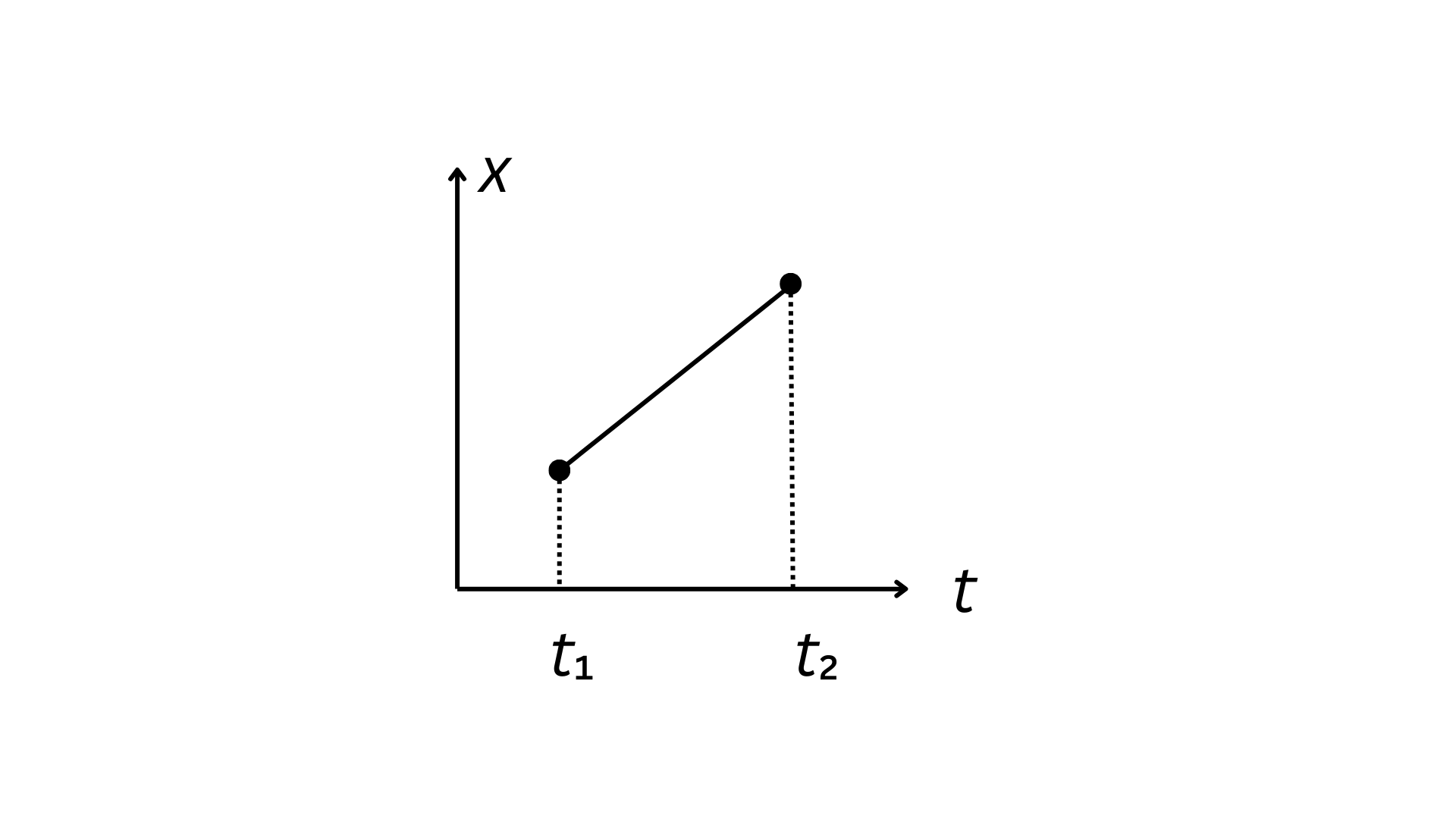 
Alternatywną trajektorią (Trajektorią nazywam krzywą \(x(t)\) kreśloną podczas ruchu ciała.) jest np ta przedstawiona na poniżej 
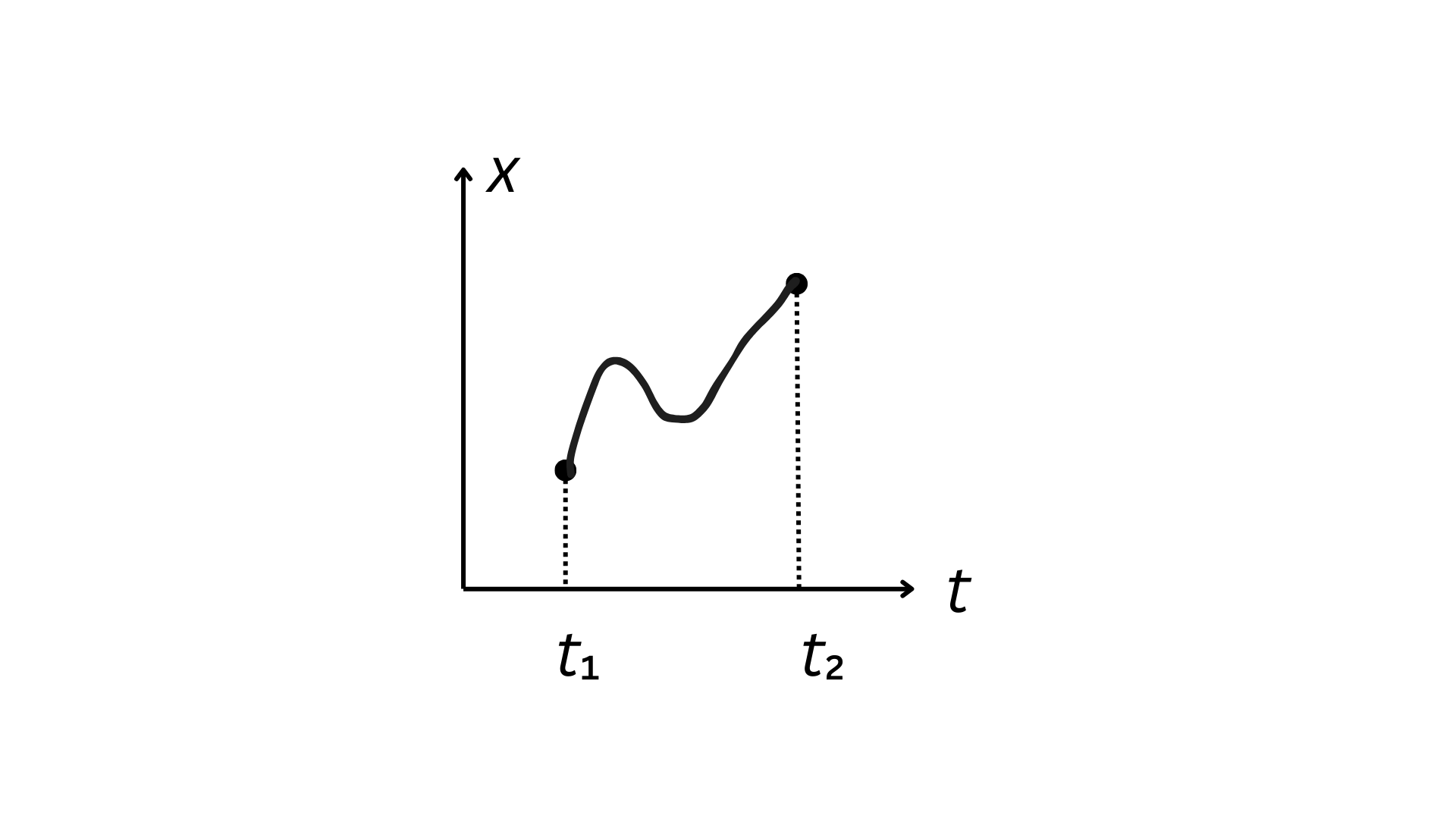W ogólnym przypadku, dla ciała poruszającego się z szybkością \(v\), jego średnia energia kinetyczna jest proporcjonalna do \(\langle v^2 \rangle\). Ze względu na to, że średnia kwadratu jest zawsze większa lub równa od kwadratu średniej, dostajemy \(\langle v^2 \rangle \geq \langle v \rangle^2 = \left( \frac{x_2-x_1}{t_2-t_1} \right)^2= v_0^2,\) zatem faktycznie działanie ma wartość minimalną dla ciała poruszającego się ze stałą prędkością.
Nieco ciekawszym przykładem jest ruch ciała w pod wpływem grawitacji. Wyobraźmy sobie piłkę, którą podrzucamy w górę. Wówczas ruch ciała odbywa się po paraboli (poniżej), zaś działanie jest opisane przez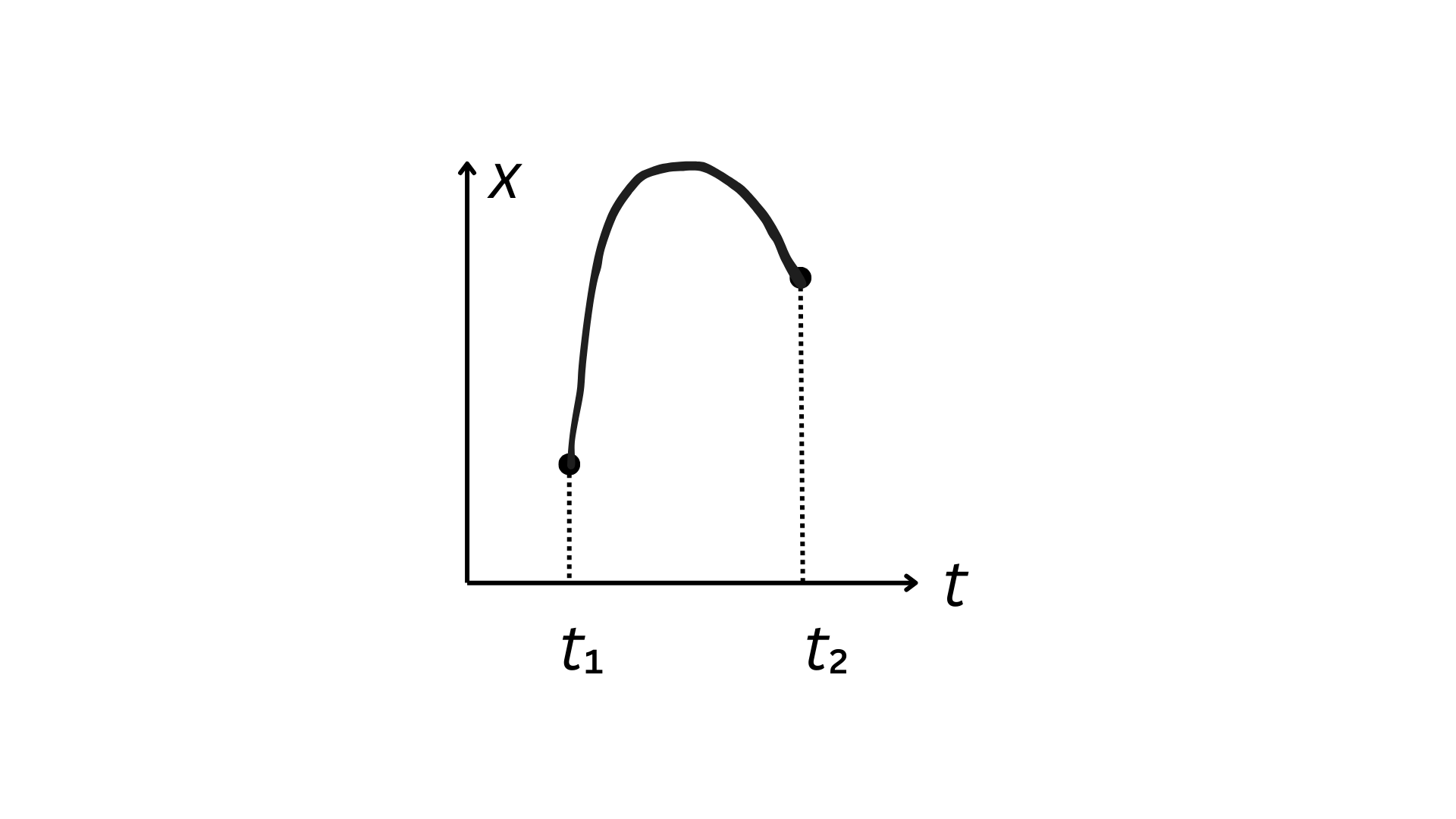 
\begin{equation} S = \int_{t_1}^{t_2} \left( \frac{1}{2}m\dot{x}^2 - mgx \right) dt. \end{equation} Możemy wyobrazić sobie, że piłka ma dużą energię kinetyczną na początku ruchu. W ten sposób jest w stanie w krótkim czasie dotrzeć na dużą wysokość, gdzie z kolej wyhamowuje i spędza tam względnie dużo czasu. Dzięki temu czynnik \(-mgx\) dominuje i działanie osiąga wartość minimalną. Można zadać pytanie, dlaczego w takim razie piłka nie leci dowolnie wysoko? Musimy pamiętać, że ciało dysponuje ciągle tym samym czasem \(t_2 - t_1\) na przemieszczenie się między \(x_1\) a \(x_2\). Zatem aby piłka mogła znaleźć się na znacznej wysokości, jej prędkość na początku musiałaby być bardzo duża, czyli również duży byłby wkład czynnika \(\frac{1}{2}m\dot{x}^2\). W ten oto sposób widzimy, że natura utrzymuje w pewnym sensie ,,idealny balans’’ między energią kinetyczną i potencjalną, który pozwala na zminimalizowanie działania. (Oczywiście nie jest do bynajmniej dowód tego, że trajektorią jest parabola, a nie jakaś inna podobna krzywa).
Równanie Eulera-Lagrange’a
Wyprowadzimy teraz równanie różniczkowe, które rozwiązuje problem szukania minimum \(S\) dla ciała poruszającego się między punktami \((t_1, x_1)\) i \((t_2, x_2)\). Powiedzmy, że \(S\) przyjmuje minimum dla \(x(t)\). Oczekujemy więc, że dla dowolnej innej krzywej \(\bar{x}(t)\) ,,w bliskim otoczeniu’’ \(x(t)\) dostaniemy \(S[\bar{x}] \geq S[x]\). Otoczenie \(x(t)\) możemy zdefiniować jako \(\bar{x}(t) = x(t) + \epsilon \eta(t)\), gdzie \(\epsilon\) jest małe, a \(\eta(t)\) jest dowolną funkcją, która zeruje się w \(t_1\) i \(t_2\)[\(\bar{x}(t) - x(t)\) to tzw. wariacja \(x(t)\).]; patrz poniżej.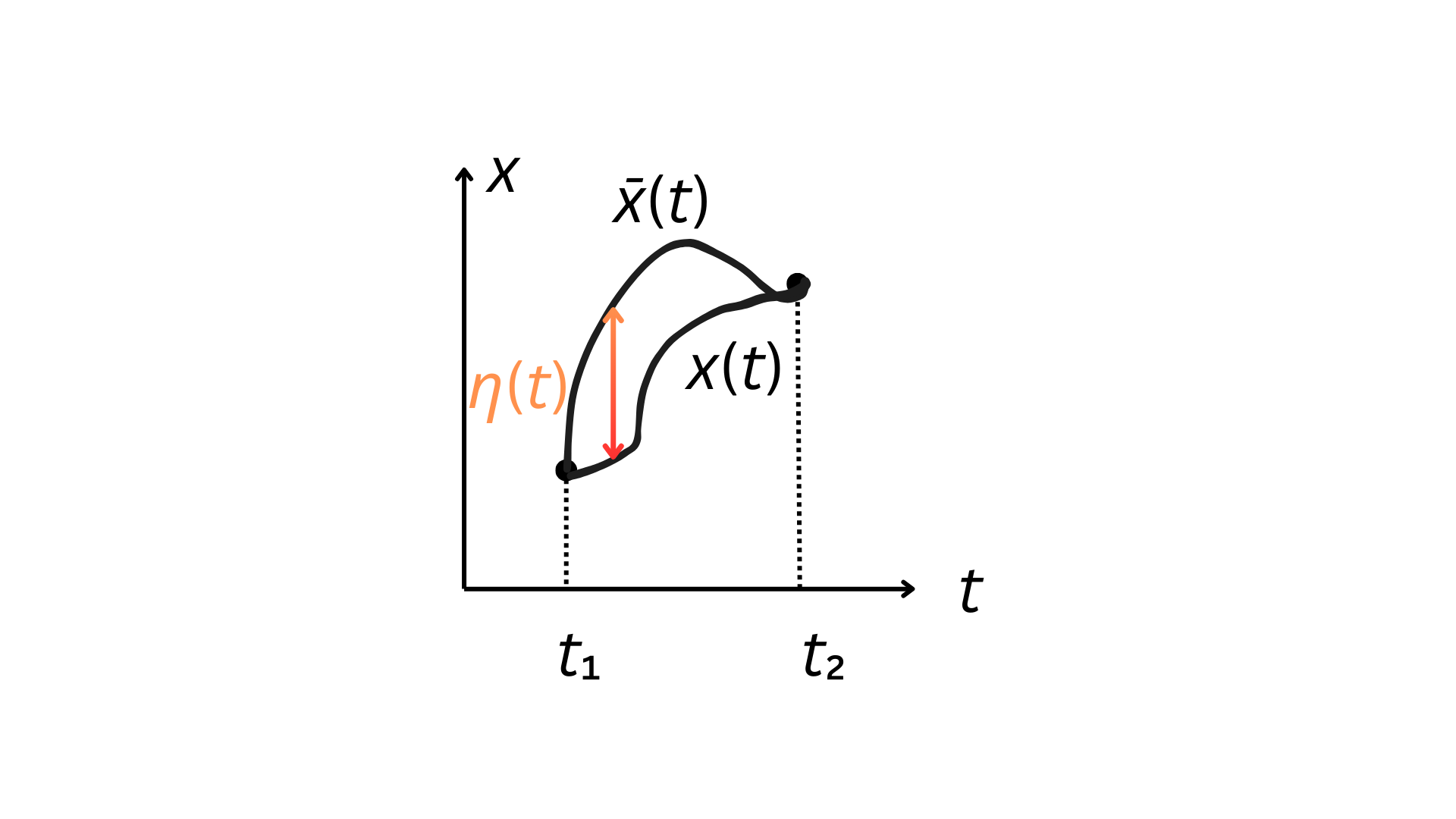 
Wynika stąd, że \(S[\bar{x}]\) jest funkcją jednej zmiennej \(\epsilon\). Ponieważ interesuje nas co dzieje się przy niewielkich zmianach \(\epsilon\), \(S[\bar{x}]\) możemy przybliżyć ograniczając się do wyrazów pierwszego rzędu:
czyli \(S[\bar{x}]\) jest proporcjonalne do \(\epsilon\). Oznacza to, że warunkiem koniecznym do tego, aby dla \(x(t)\) istniało minimum [Ogólnie ekstremum.] jest \begin{equation} \left(\frac{dS}{d\epsilon} \right)_0 = 0. \end{equation} Oznaczmy różnicę \(T - V\) przez \(L\), wówczas \(dS/d\epsilon\) jest równe
\[\frac{d}{d\epsilon} \int_{t_1}^{t_2} L(\bar{x}, \dot{\bar{x}}, t) dt = \int_{t_1}^{t_2} \frac{d}{d\epsilon} L(\bar{x}, \dot{\bar{x}}, t) dt\\ = \int_{t_1}^{t_2} \left( \frac{\partial L}{\partial \bar{x}} \frac{d\bar{x}}{d\epsilon} + \frac{\partial L}{\partial \dot{\bar{x}}} \frac{d\dot{\bar{x}}}{d\epsilon} + \frac{\partial L}{\partial t} \frac{dt}{d\epsilon} \right) dt = \int_{t_1}^{t_2} \left( \frac{\partial L}{\partial \bar{x}} \eta + \frac{\partial L}{\partial \dot{\bar{x}}} \dot{\eta} \right) dt.\]Obliczając w \(\epsilon = 0\) otrzymujemy
\[\int_{t_1}^{t_2} \left( \frac{\partial L}{\partial x} \eta + \frac{\partial L}{\partial \dot{x}} \dot{\eta} \right) dt = 0.\]Drugi składnik całkujemy przez części otrzymując
\[\int_{t_1}^{t_2} \frac{\partial L}{\partial \dot{x}} \dot{\eta} dt = \left( \frac{\partial L}{\partial \dot{x}} \eta \right)_{t_1}^{t_2} - \int_{t_1}^{t_2} \left( \eta \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} \right) dt.\]Pierwszy składnik znika, bo \(\eta\) w \(t_1\) i \(t_2\) jest równa zero. Ostatecznie otrzymujemy
\[\int_{t_1}^{t_2} \left( \frac{\partial L}{\partial x} - \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} \right) \eta dt = 0.\]Ponieważ \(\eta\) była dowolną funkcją, oznacza to, że \begin{equation} \label{eq:el} \frac{\partial L}{\partial x} - \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} = 0. \end{equation} Równanie to nazywamy równaniem Eulera-Lagrange’a.
Podstawmy \(L = T - V = \frac{1}{2}m\dot{x}^2 - V(x, t)\) do powyższego równania. Otrzymujemy wówczas \[ -\frac{\partial V}{\partial x} - \frac{d}{dt}(m\dot{x} - 0) = 0, \] czyli \begin{equation} -\frac{\partial V}{\partial x} = m\ddot{x}. \end{equation} Otrzymaliśmy więc, że zasada najmniejszego działania jest równoważna II prawu dynamiki Newtona [Z pozoru tylko dla sił zachowawczych, ale tak naprawdę wszystkie siły są zachowawcze.].
Przykłady zastosowania
Opisanie ruchu ciała za pomocą równania E-L ma kilka zalet.
Po pierwsze, interesują nas jedynie energia kinetyczna i potencjalna, które są wartościami skalarnymi, a nie siły, które są wektorami.
Dodatkowo ruch cząstki może być z góry ograniczony (np. ruch wahadła). W sformułowaniu Newtona należy wówczas wziąć pod uwagę siły związane z narzuconymi ograniczeniami (np. siła naprężenia nici). W sformułowaniu Lagrange’a powoduje to jedynie zmniejszenie wymiarowości problemu poprzez odpowiedni dobór zmiennych. Dla wspomnianego wahadła (powiedzmy, że ma długość \(l\) i masę \(m\)), interesuje nas trajektoria \(\phi(t)\) (kąt wychylenia) między danymi dwoma punktami \((t_1, \phi_1)\) i \((t_2, \phi_2)\). Zauważmy, że równanie E-L jest niezależne od zmiennej, jaką opisujemy ruch, zatem opisanie ruchu wahadła sprowadza się do znalezienia wyrażenia na \(T\) i \(V\). W tym przypadku są to \(T = (1/2)ml^2\phi^2\) oraz \(V = mgl(1 - \cos(\phi))\). Po zastosowaniu równania E-L dostajemy oczekiwane równanie ruchu \[\ddot{\phi} - \frac{g}{l} \sin(\phi) = 0.\]
Równania E-L możemy również użyć do rozwiązania innych problemów optymalizacyjnych polegających sprowadzających się do znalezienia ekstremum danego funkcjonału [Funkcjonałem nazywam tutaj ,,funkcję funkcji’’ postaci \(\int_{t_1}^{t_2}F(x,\dot{x}, t) dt\), gdzie \(x = x(t)\).] przy określonych ,,warunkach brzegowych’’.
Na przykład możemy określić jaki kształt powinna mieć krzywa, po której ciało pod wpływem stałej siły (siły ciężkości) stacza się w możliwie najkrótszym czasie (jest to tzw. problem brachistochrony).
Można pokazać, że sumaryczny czas w ruchu po krzywej \(y(x)\) pomiędzy punktami \((x_1, y(x_1))\) i \((x_2, y(x_2))\) wynosi \[ t_{12} = \int_{x_1}^{x_2} \frac{\sqrt{1 + \dot{y}^2}}{\sqrt{2gy}}dx. \] Stosując równanie E-L dla \(L(y,\dot{y},x) = \frac{\sqrt{1 + \dot{y}^2}}{\sqrt{2gy}}\) otrzymujemy \[ x = a(\phi - \sin(\phi)), y = a(1 - \cos(\phi)). \] Jest to równanie cykloidy (krzywa wyznaczona przez toczące się koło o promieniu \(a\); \(\phi\) jest kątem obrotu).
Interpretacja Feynmana
Według Newtona, w każdym punkcie toru ruchu cząstki działają na nią siły, które sprawiają, że porusza się w tym, a nie innym kierunku. Zatem jest to zasada w pewnym sensie lokalna. Z drugiej strony, zasada najmniejszego działania jest zasadą globalną. Cząstka wybiera ruch po określonej trajektorii, ponieważ zminimalizuje ona działanie. Skąd jednak cząstka wie z góry, która trajektoria będzie tą odpowiednią? Według Feynmana odpowiedzi należy szukać w mechanice kwantowej.
Prawdopodobieństwo tego, że cząstka przemieści się z punktu \((t_1, x_1)\) do \((t_2, x_2)\) jest równe kwadratowi amplitudy prawdopodobieństwa. Ta zaś jest równa sumie amplitud dla każdej możliwej trajektorii łączącej \((t_1, x_1)\) z \((t_2, x_2)\). Dla określonej trajektorii jest ona proporcjonalna do \(e^{iS/\hbar}\). Powiedzieliśmy już, że dla trajektorii leżących bardzo blisko tej, która minimalizuje działanie, różnica w działaniu uwidacznia się dopiero w wyrażeniu drugiego rzędu, zaś dla wszystkich pozostałych par, ta różnica jest widoczna w wyrażeniach pierwszego rzędu. Ze względu na to, że \(S\), z którym mamy do czynienia w mechanice klasycznej jest o rzędy wielkości większe od \(\hbar\), trajektorie nieleżące w pobliżu optimum (nawet bardzo do siebie zbliżone) dają zupełnie inne wartości amplitudy, zatem częściowa suma odpowiadających im amplitud jest w zasadzie zerowa. Z drugiej strony, sumując amplitudy odpowiadające trajektoriom w pobliżu tej optymalnej dostajemy niezerową wartość.
Oznacza to, że prawdopodobieństwo tego, że cząstka poruszać się będzie po trajektorii, która nie minimalizuje działania jest w zasadzie zerowe.
Jeśli więc przyjmiemy, że z cząstką związana jest pewna fala prawdopodobieństwa, to możemy uznać, że jej trajektoria jest następstwem nakładania się tej fali ze samą sobą. W pewnym więc sensie cząstka porusza się po wszystkich możliwych trajektoriach równocześnie.
Bibliografia
- The Feynman Lectures on Physics, R. Feynman
- Classical Mechanics, H. Goldstein, C. P. Poole, J. F. Safko
- Mechanics, L. D. Landau, E. M. Lifshitz